Pickstock

Importing Modules

The gamspy Python package is loaded in order to access GAMSPy syntax.

from gamspy import Container, Set, Alias, Parameter, Variable, Equation, Model, Sum, Sense, Card, Options

Loading the price data

The price data is provided from a CSV file located on the web. The Python package pandas is used to load the data.

import pandas as pd

url = (
    "https://github.com/daveh19/pydataberlin2017/raw/master/notebooks/dowjones2016.csv"
)
price_data = pd.read_csv(url)

m = Container()
date = Set(m, "date", description="trading date")
symbol = Set(m, "symbol", description="stock symbol")
price = Parameter(
    m,
    "price",
    [date, symbol],
    domain_forwarding=True,
    records=price_data,
    description="price of stock on date",
)
d = Alias(m, "d", date)
s = Alias(m, "s", symbol)

price.records.head()

	date	symbol	value
0	2016-01-04	AAPL	105.349998
1	2016-01-04	AXP	67.589996
2	2016-01-04	BA	140.500000
3	2016-01-04	CAT	67.989998
4	2016-01-04	CSCO	26.410000

The mean price per stock is calculated in GAMS.

avgprice = Parameter(m, "avgprice", symbol, description="average price of stock")
avgprice[s] = Sum(d, price[d, s]) / Card(d)

avgprice.records.head()

	symbol	value
0	AAPL	104.604008
1	AXP	63.793333
2	BA	133.111508
3	CAT	78.698016
4	CSCO	28.789683

The averages can be used in order to calculate weights.

weight = Parameter(m, "weight", symbol, description="weight of stock")
weight[symbol] = avgprice[symbol] / Sum(s, avgprice[s])
weight.records.head()

	symbol	value
0	AAPL	0.039960
1	AXP	0.024370
2	BA	0.050850
3	CAT	0.030063
4	CSCO	0.010998

Compute the contributions using weight and price

contribution = Parameter(m, "contribution", [date, symbol])
contribution[d, s] = weight[s] * price[d, s]
contribution.records.head()

	date	symbol	value
0	2016-01-04	AAPL	4.209752
1	2016-01-04	AXP	1.647143
2	2016-01-04	BA	7.144396
3	2016-01-04	CAT	2.044007
4	2016-01-04	CSCO	0.290455

Compute index values

index = Parameter(m, "index", date, description="Dow Jones index")
index[d] = Sum(s, contribution[d, s])
index.records.head()

	date	value
0	2016-01-04	100.572929
1	2016-01-05	100.511422
2	2016-01-06	99.014207
3	2016-01-07	96.606033
4	2016-01-08	95.685461

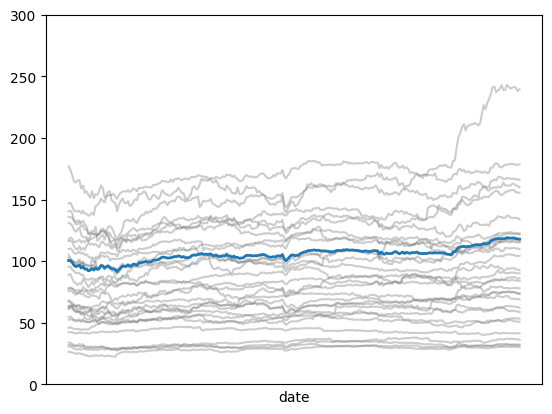
Create a plot showing the symbol and index values over time

import matplotlib
import matplotlib.pyplot as plt

fig, ax = plt.subplots()
price.records.groupby("symbol", observed=True).plot(
    x="date",
    y="value",
    ax=ax,
    alpha=0.4,
    color="grey",
    legend=False,
    ylim=(0, 300),
    xticks=[],
)
index.records.plot(x="date", y="value", ax=ax, linewidth=2, legend=False)

<Axes: xlabel='date'>

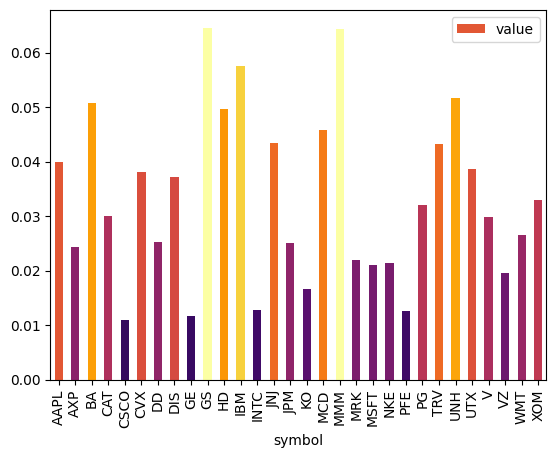
sMap = matplotlib.cm.ScalarMappable(
    norm=matplotlib.colors.Normalize(0, weight.records["value"].max()), cmap="inferno"
)
color = [sMap.to_rgba(x) for x in weight.records["value"]]
weight.records.plot.bar(x="symbol", y="value", color=color)

<Axes: xlabel='symbol'>

Define dynamic set ds and scalar maxstock.

trainingdays = Parameter(m, "trainingdays", records=100)
maxstock = Parameter(m, "maxstock", records=3)
ds = Set(m, "ds", date, description="selected dates")
ds.setRecords(date.records["uni"][:100])

Declaration of the variables and equations used to formulate the optimization model

p = Variable(m, "p", "binary", symbol, description="is stock included?")
w = Variable(m, "w", "positive", symbol, description="what part of the portfolio")
slpos = Variable(m, "slpos", "positive", date, description="positive slack")
slneg = Variable(m, "slneg", "positive", date, description="negative slack")

Defining the actual model

We know come to the decision problem, where we want to pick a small subset of the stocks together with some weights, such that this portfolio has a similar behavior to our overall Dow Jones index.

The model is based on a linear regression over the time series, but we minimize the loss using the L1-norm (absolute value), and allow only a fixed number of weights to take nonzero variable.

\begin{align} \text{minimize} \qquad & \text{obj}:= \sum_{ds} \text{slpos}_{ds} + \text{slneg}_{ds} \\ \text{subject to} \qquad & \sum_{s} \text{price}_{ds, s} \cdot w_{s} = \text{index}_{ds} + \text{slpos}_{ds} - \text{slneg}_{ds} & (\forall{ds}) \\ & w_{s} \leq p_{s} & (\forall{s}) \\ & \sum_{s}{p_{s}} \leq \text{maxstock} \\ & w_{s}\geq 0, \qquad p_{s}\in \{0,1\} & (\forall s) \\ & \text{slpos}_{d}\geq 0, \qquad \text{slneg}_{d}\geq 0 & (\forall d) \end{align}

fit = Equation(m, name="deffit", domain=[ds], description="fit to Dow Jones indeex")
fit[ds] = Sum(s, price[ds, s] * w[s]) == index[ds] + slpos[ds] - slneg[ds]

pick = Equation(
    m, name="defpick", domain=[s], description="can only use stok if picked"
)
pick[s] = w[s] <= p[s]

numstock = Equation(m, name="defnumstock", description="few stocks allowed")
numstock[...] = Sum(s, p[s]) <= maxstock

Objective

obj = Sum(ds, slpos[ds] + slneg[ds])

Model

pickstock = Model(
    container=m,
    name="pickstock",
    equations=m.getEquations(),
    problem="MIP",
    sense=Sense.MIN,
    objective=obj,
)

Specify ‘maxstock’ and ‘trainingdays’ and solve the model.

ds.setRecords(date.records["uni"][:100])
maxstock.setRecords(3)

Solve

pickstock.solve(options=Options(relative_optimality_gap=0.01, time_limit=6))

	Solver Status	Model Status	Objective	Num of Equations	Num of Variables	Model Type	Solver	Solver Time
0	Normal	Integer	45.5725938967286	132	261	MIP	CPLEX	0.142

Generate reporting parameters

fund = Parameter(m, "fund", [date], description="Index fund report parameter")
fund[d] = Sum(s, price[d, s] * w.l[s])
error = Parameter(m, "error", [date], description="Absolute error")
error[d] = index[d] - fund[d]

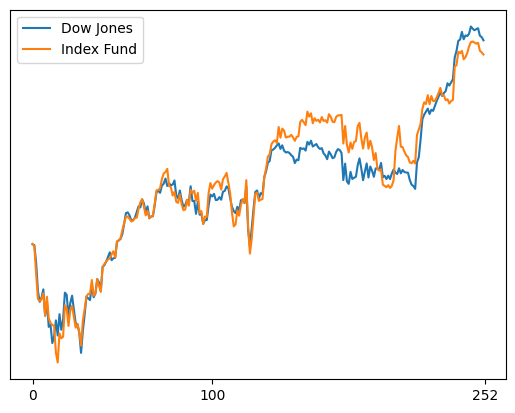
Plotting of the results

fig, ax = plt.subplots()
trainingDays = int(trainingdays.records.iloc[0].to_list()[0])
index.records.plot(
    y="value",
    ax=ax,
    xticks=[0, trainingDays, len(date.records)],
    yticks=[],
    label="Dow Jones",
)
fund.records.plot(
    y="value",
    ax=ax,
    xticks=[0, trainingDays, len(date.records)],
    yticks=[],
    label="Index Fund",
)

<Axes: >

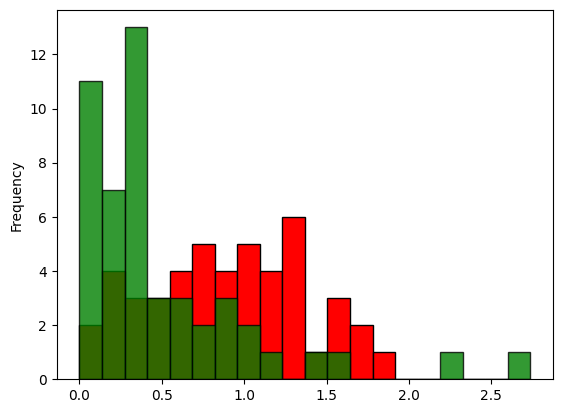
maxError = error.records["value"].max()
fig, ax = plt.subplots(edgecolor="black")
error.records["value"][trainingDays:].plot.hist(
    x="date",
    y="value",
    ax=ax,
    bins=20,
    range=(0, maxError),
    label="later",
    color="red",
    edgecolor="black",
)
error.records["value"][:trainingDays].plot.hist(
    x="date",
    y="value",
    ax=ax,
    bins=20,
    range=(0, maxError),
    label="training",
    color="green",
    alpha=0.8,
    edgecolor="black",
)

<Axes: ylabel='Frequency'>